이분 그래프란?
인접한 정점끼리 서로 다른 두가지 집합으로만 나눈 그래프를 의미한다.

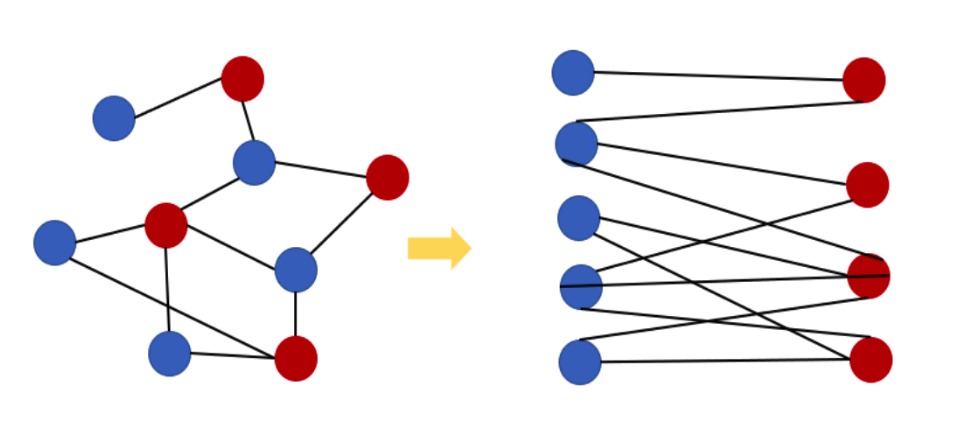
위 그림과 같이 모든 정점이 두 집합으로 나뉘고(여기서는 서로 다른 두 색상으로 구별한다.) 같은 집합끼리는 인접하지 않는 그래프의 형태이다.
이분 그래프의 특징
- 한 간선의 양 끝 정점은 서로 다른 집합에 속해 있어야 한다.
- 같은 집합의 정점끼리는 하나의 간선으로 이어질 수 없다.
- Cycle이 발생했을 때, 그 Cycle을 잇는 간선의 개수는 짝수여야 한다.
- 간선이 없고 정점만 있는 그래프도 이분 그래프이다.
이분 그래프 판별볍
이분 그래프 여부를 판별하기 위해서는 보통 DFS나 BFS로 그래프를 탐색하면서 판별한다.
1. BFS , DFS 를 수행하며 각 정점을 방문할때 마다 인접한 그룹과 다른 색으로 칠한다.
2. 각 정점을 방문 중, 자신과 인접한 정점의 색이 자신과 같다면 그 그래프는 이분 그래프가 아니다. (발견과 동시에 탐색 종료)
3. 모든 정점을 방문하고 인접한 정점끼리 같은색이 없다면 이분그래프이다.
참고로 모든 정점을 다 방문하며 탐색하기 때문에 시간복잡도는 O(V+E)를 따른다.
728x90
'Data Structure' 카테고리의 다른 글
| [자료구조] 최소 신장 트리 Minimum Spanning Tree (0) | 2024.01.10 |
|---|---|
| [자료구조] 이진탐색트리 Binary Search Tree (0) | 2024.01.05 |
| Deque 자료구조 예제 및 정리 (0) | 2023.11.02 |
| Queue 자료구조 예제 및 정리 (0) | 2023.11.02 |
| Stack 자료구조 예제 및 정리 (0) | 2023.11.02 |