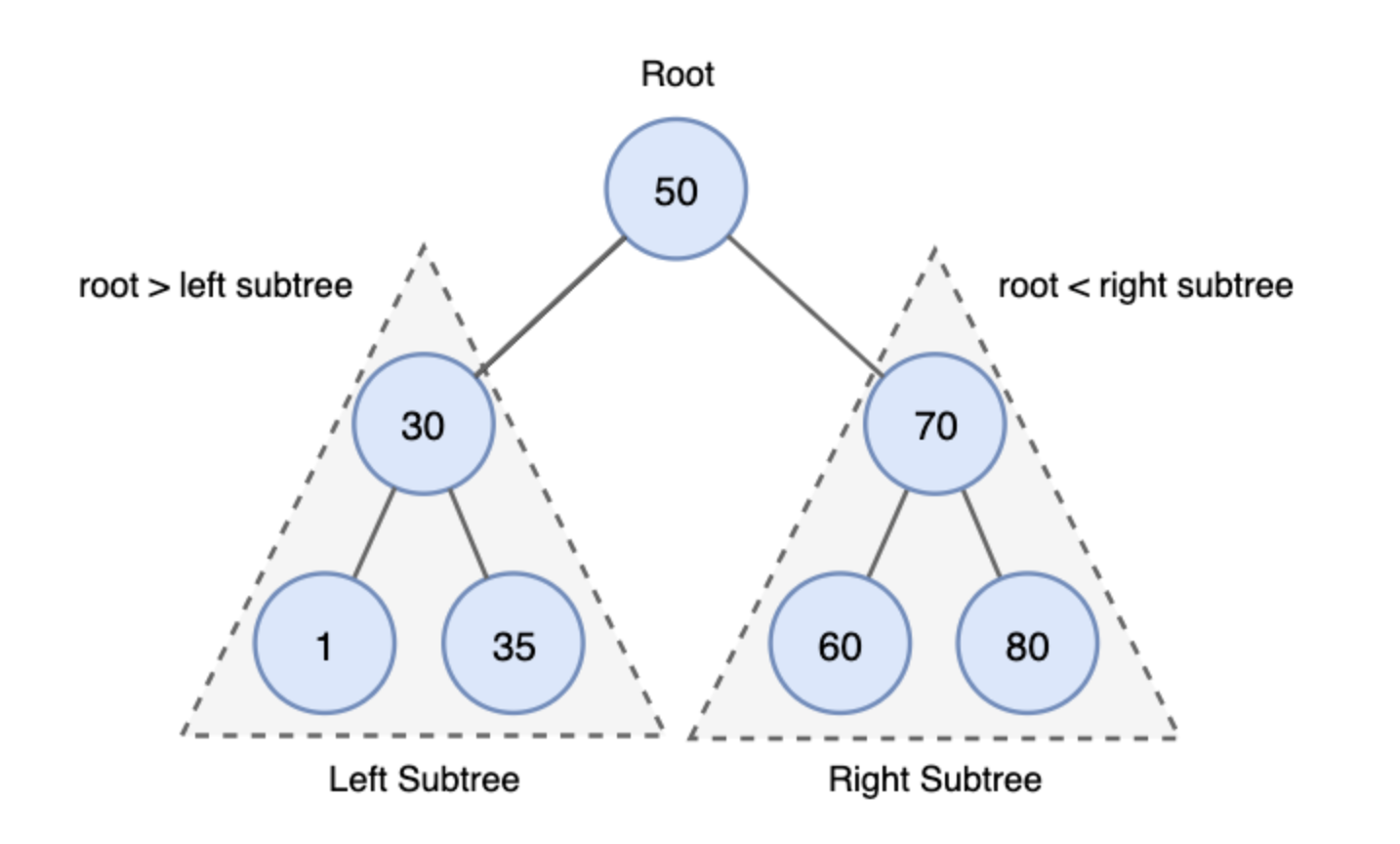
이진탐색트리(Binary Search Tree, BST)는 널리 사용되는 형태의 이진트리이다. BST는 다음과 같은 속성있다.
부모 노드의 값 >= 왼쪽 자식 노드의 값
부모 노드의 값 <= 오른쪽 자식 노드의 값
즉, (왼쪽 노드 <= 부모 노드 <= 오른쪽 노드)의 관계를 가진다.
이와 같은 관계 때문에, 원소 검색을 위해 루트 노드부터 차례대로 값을 비교하는 경우, 각 단계마다 검색 범위가 절반으로 줄어들게 된다는 특징이 있다.
이진 탐색 트리는 노드의 개수가 N개일 경우 탐색, 노드 삽입, 노드 제거에 평균적인 경우 O(log(N))의 시간복잡도를, 최악의 경우 O(N)의 시간복잡도를 가진다.
- BST의 삽입
50 15 62 70 7 54 11
1. 맨 첫번째를 트리의 루트로 삽입
2. 순차적으로 순회하며 루트보다 작으면 왼쪽에 삽입
3. 그렇지 않으면 오른쪽에 삽입

- BST의 검색
1. 루트에서 시작
2. 검색값을 루트와 비교 후, 작으면 왼쪽으로, 크면 오른쪽으로 재귀
3. 찾을때까지 계속 반복
4. 찾는 값이 없으면 NULL을 리턴하고 종료
60을 찾는 과정
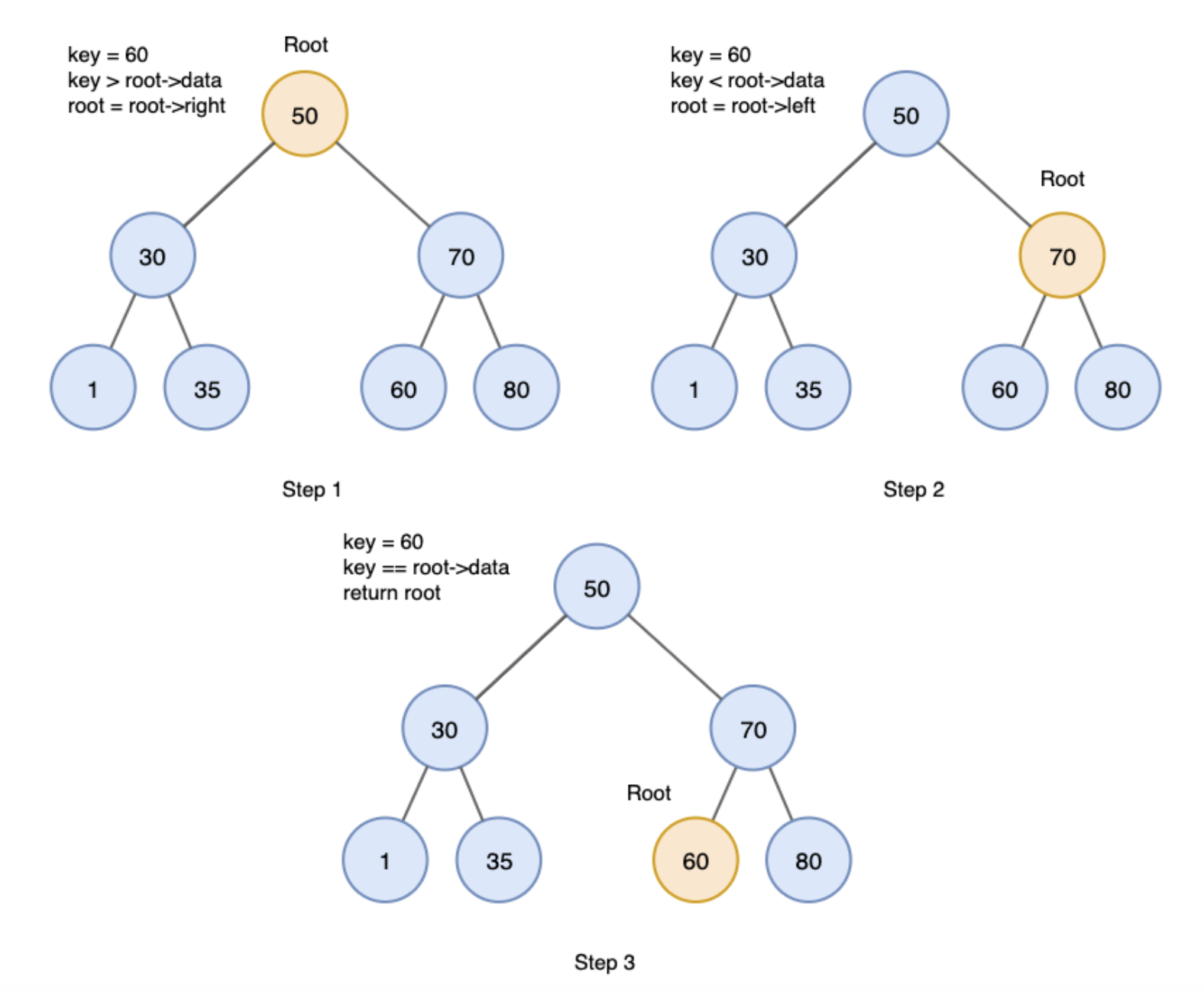
- BST의 삭제
총 3가지의 경우로 나뉜다.
1. 삭제하려는 노드가 리프 노드(자식이 하나도 없는 맨 끝단 노드)일 경우
그냥 지우면 된다.

2. 삭제하려는 노드가 자식이 하나일 경우
삭제할 노드를 삭제하고, 삭제된 노드의 자식을 삭제한 노드의 부모와 직접 연결한다. 이미 정렬이 된 상태였기 때문에 서로 고쳐주기만 하면 끝난다.

3. 삭제하려는 노드가 자식이 둘일 경우
이 경우에는, 그 두 자식의 중간값인 노드를 새로 찾는 과정이 추가된다. 제일 까다로운 경우이다.

- 코드 구현
#include <iostream>
using namespace std;
struct node {
int data;
node* left;
node* right;
};
struct BST {
node* root = nullptr;
node* find(int value) {
return find_impl(root, value); //탐색 함수 콜
}
private:
node* find_impl(node* current, int value) {
if (!current) {
cout << endl;
return NULL;
}//current가 비어있으면 NULL return
if (current->data == value) {
cout << value << " 을/를 찾았습니다!" << endl;
return current;
}//current가 바로 찾는값이면 current를 리턴하고 종료
else if (value < current->data) {
cout << current->data << " 에서 왼쪽으로 이동 - ";
return find_impl(current->left, value);
}//찾는 값이 더 작으면 왼쪽으로 이동
else if (current->data < value) {
cout << current->data << " 에서 오른쪽으로 이동 - ";
return find_impl(current->right, value);
}//찾는 값이 더 크면 오른쪽으로 이동
}
//노드 탐색
public:
void insert(int value) {
if (!root) root = new node {value, NULL, NULL}; //root가 비어있으면 새로 생성해서 삽입
else insert_impl(root, value); //아니면 삽입 함수 콜
}
private:
void insert_impl(node* current, int value) {
if (value < current->data) {
if (!current->left) current->left = new node {value, NULL, NULL};
else insert_impl(current->left, value);
} //생성할 값이 더 작으면 왼쪽 노드로 순회하여 재귀
else {
if (!current->right) current->right = new node {value, NULL, NULL};
else insert_impl(current->right, value);
} //생설할 값이 더 크면 오른족 노드로 순회하여 재귀
}
//노드 삽입
public:
void inorder() {
inorder_impl(root);
}
private:
void inorder_impl(node* start) {
if (!start) return;
inorder_impl(start->left);
cout << start->data << ' ';
inorder_impl(start->right);
} //중위 순회
public:
node* successor(node* start) {
auto current = start->right; //먼저 현재 노드에서 오른쪽으로 이동 후,
while(current && current->left)
current = current->left; //그 중에서 제일 왼쪽 끝단으로 감.
return current; //그러고 return.
} //후속노드 찾는 함수. 후속노드란, 삭제하려고 하는 노드 다음으로 큰 숫자를 가진 노드. 즉, 현재 노드보다 큰 노드들 중에서 가장 작은 노드를 말함.
//이를 구하려면, 현재 노드에서 오른쪽으로 이동 후, 그 중에서 제일 왼쪽 끝단으로 가면 찾을 수 있음. 그 매커니즘을 구현하는 함수가 바로 successor.
void deleteValue(int value) {
root = delete_impl(root, value); //삭제 함수 콜
}
private:
node* delete_impl(node* start, int value) {
if (!start) return NULL; //아예 비어있는 트리면 NULL return
if (value < start->data) start->left = delete_impl(start->left, value);
else if (start->data < value) start->right = delete_impl(start->right, value);
else {
if (!start->left) {
auto tmp = start->right;
delete start;
return tmp;
} //오른쪽 자식 노드만 있으면 자식노드는 tmp로 살려두고 return하여 최종적으로는 부모노드에 연결해준다.
if (!start->right) {
auto tmp = start->left;
delete start;
return tmp;
} //왼쪽 자식 노드만 있으면 자식노드는 tmp로 살려두고 return하여 최종적으로는 부모노드에 연결해준다.
//자식이 둘 다 있을경우, 위의 후속노드를 활용하여 succNode에 넣어놓고, 삭제하려는 대상이 지워진 위치에 그대로 가져다 넣는다.
auto succNode = successor(start);
start->data = succNode->data;
start->right = delete_impl(start->right, succNode->data);
//그 이후, 후속노드의 자식노드가 있다면, 지워준다. 이때, 자식노드가 있다면 그 노드는 무조건 오른쪽 노드임을 명심하자!
//왼쪽 노드가 존재하는 후속노드는 애초에 존재할 수 없다. 그랬다면, 후속노드는 그 본인이 아니라 자식으로 딸린 왼쪽노드가 후속노드일것이기 때문!
}
return start;
}
//노드 삭제
};
int main() {
BST tree;
tree.insert(12);
tree.insert(10);
tree.insert(20);
tree.insert(8);
tree.insert(11);
tree.insert(15);
tree.insert(28);
tree.insert(4);
tree.insert(2);
cout << "중위 순회 : ";
tree.inorder();
cout << endl;
cout << "삭제할 노드를 입력하세요 : ";
int a;
cin >> a;
tree.deleteValue(a);
cout << a << " 을/를 삭제한 후, 중위 순회 : ";
tree.inorder();
cout << endl;
cout << "찾을 노드를 입력하세요 : ";
int b;
cin >> b;
if (tree.find(b)) cout << b << " 은/는 트리에 있습니다!" << endl;
else cout << b << " 은/는 트리에 없습니다." << endl;
return 0;
}728x90
'Data Structure' 카테고리의 다른 글
| [자료구조] 이분 그래프 Bipartite Graph (0) | 2024.02.25 |
|---|---|
| [자료구조] 최소 신장 트리 Minimum Spanning Tree (0) | 2024.01.10 |
| Deque 자료구조 예제 및 정리 (0) | 2023.11.02 |
| Queue 자료구조 예제 및 정리 (0) | 2023.11.02 |
| Stack 자료구조 예제 및 정리 (0) | 2023.11.02 |