다익스트라 알고리즘이란?
음수 가중치가 없는 그래프에서 동작하는 최단 경로 탐색 알고리즘이다. 한 정점에서 다른 정점까지의 최단 경로를 구하는데, 이 과정에서 도착 정점 뿐만 아니라 모든 다른 정점까지 최단 경로로 방문하며 각 정점까지의 최단 경로를 모두 찾게 된다. 매번 최단 경로의 정점을 선택해 탐색을 반복하는 것이다.
그래프 탐색 알고리즘 중 최소 비용을 구하는 알고리즘은 다익스트라 외에도 벨만-포드 알고리즘 Bellman-Ford Algorithm, 플로이드-워셜 Floyd-Warshall 알고리즘 등이 있다. (벨만-포드 알고리즘은 음수 가중치의 그래프도 탐색 가능하다.) 그중에서도 다익스트라 알고리즘은 프림 알고리즘을 살짝 변형한 형태인데, 두 가지 차이점이 존재한다. 차이점은 다음과 같다.
1. 프림 알고리즘은 경계로부터 최단 거리를 정점의 거리 값으로 설정하지만, 다익스트라 알고리즘은 시작 정점으로부터 각 정점까지의 전체 거리를 사용한다.
2. 다익스트라 알고리즘은 목적 정점이 나타나면 종료하지만, 프림 알고리즘은 모든 정점을 방문해야 종료한다.
다익스트라 알고리즘의 시퀀스
1. 처음엔 시작 정점을 방문한다.
2. 방문하지 않은 정점들 중 가장 가중치 값이 작은 정점을 방문한다.
3. 해당 정점을 거쳐서 갈 수 있는 정점의 거리가 이전에 기록한 값보다 작다면 그 거리를 갱신한다.
4. 목적지에 도달할때까지 2~3의 과정을 반복한다.
5. 목적지에 도달하면 종료한다.
글로만 이해하면 이해가 잘 안되니, 그림을 그려서 다익스트라 알고리즘을 수행해보자.

정점 1을 시작점으로 해서 각 정점까지의 최단거리를 한번 구해보자. 그래프의 가중치는 위 그림과 같고, 표에는 시작점부터 각 정점까지의 거리가 적혀있다. 맨 처음에는 아직 아무것도 정해진것이 없으니 INF, 즉 무한으로 설정한다.

정점 1을 방문했을때는 해당 정점을 거쳐 갈수있는 다른 정점들의 거리를 갱신한다. INF 보다는 작으므로 갱신된다.

그 다음으로는 방문하지 않은 정점 중 가장 최단거리의 정점을 찾아 방문한다. 정점 2까지의 거리가 3이기에 2를 방문한다. 정점 2에서 갈 수 있는 정점 4와 6의 거리를 갱신한다.
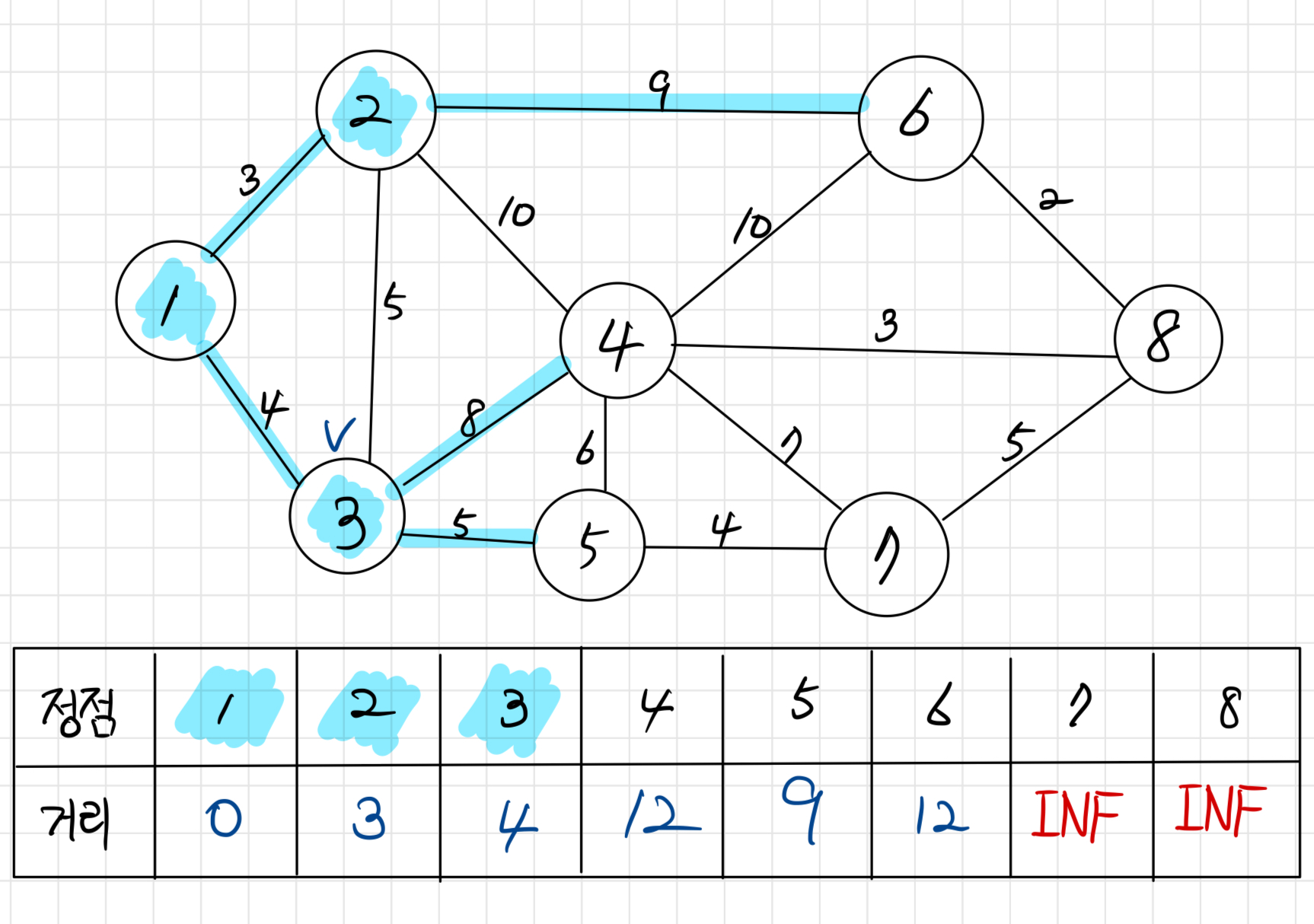
정점 3을 방문한다. 이때, 정점 4로 갈 수 있는 거리가 원래는 13이었는데, 정점 3을 거쳐서 가는 경로로 가면 거리가 12로 단축된다. 따라서 정점 4까지의 거리를 12로 갱신한다.
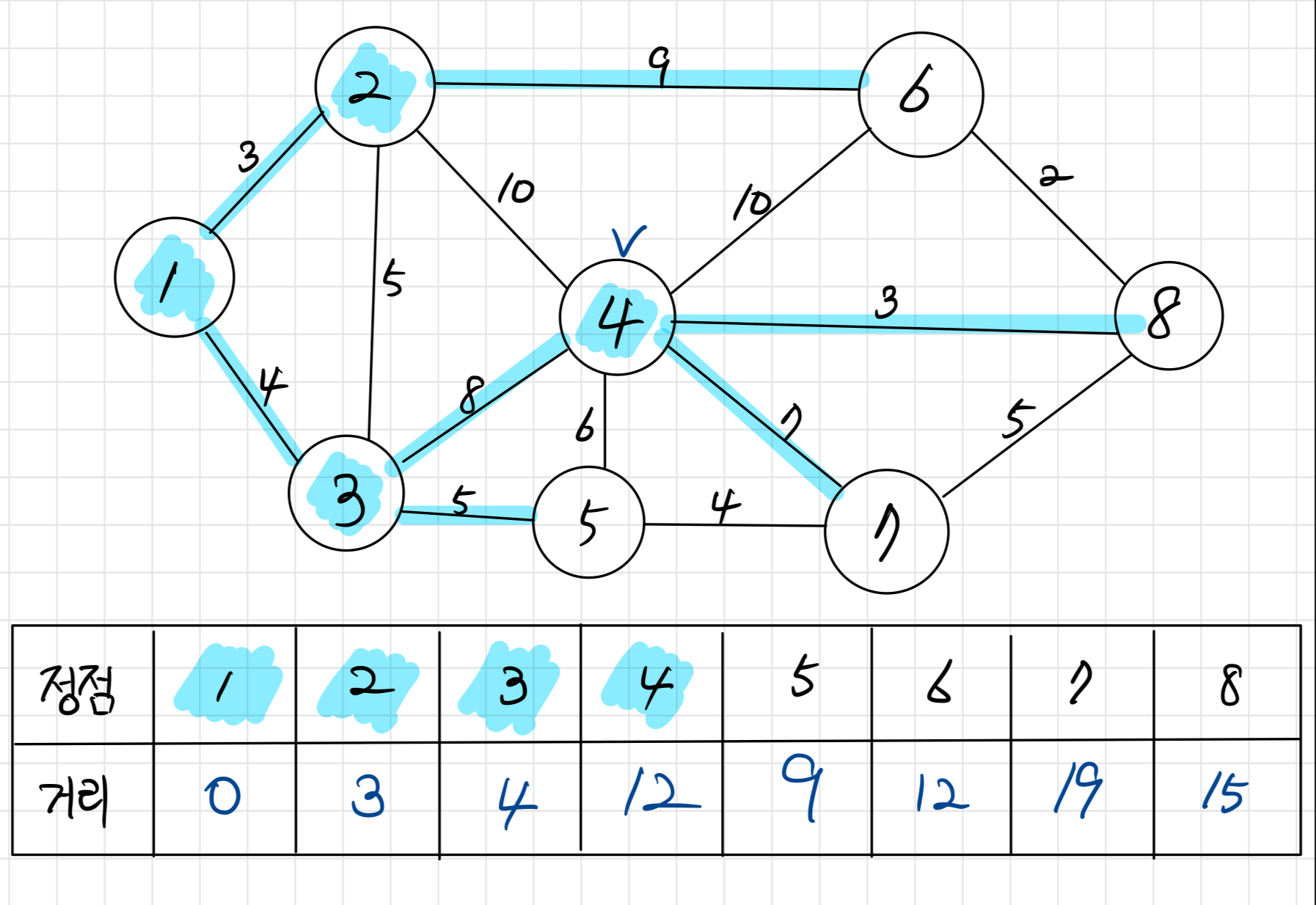
정점 4를 방문한다. 이제 모든 정점까지의 거리가 갱신되었다. 앞으로는 기존 경로보다 짧은 경로를 찾았을때만 갱신할 것이다.
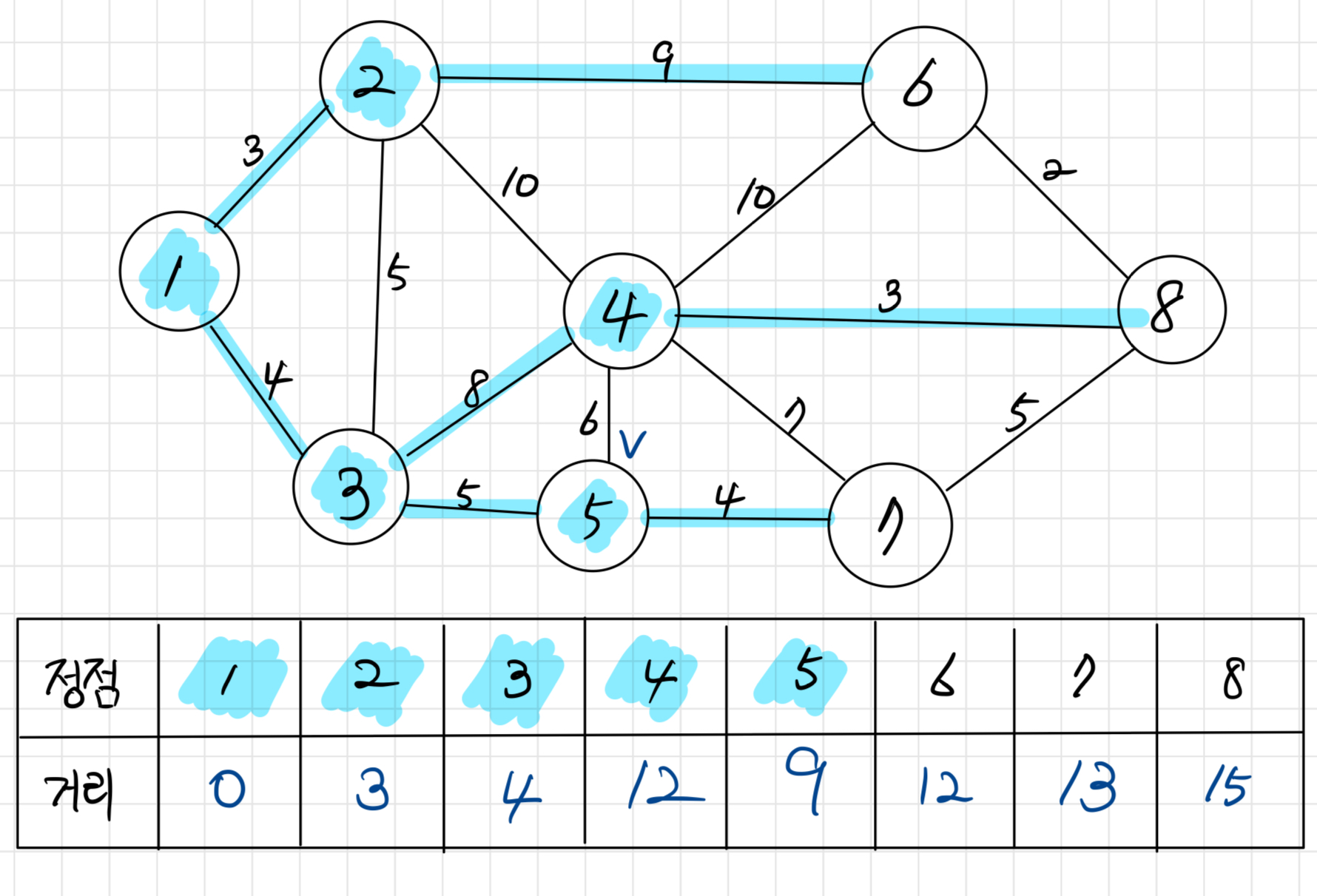
정점 5를 방문한다. 이때, 정점 7까지의 거리를 13으로 갱신한다. (기존 경로라면 19지만, 5를 경유해서 가는 경로가 13으로 더 짧다.)
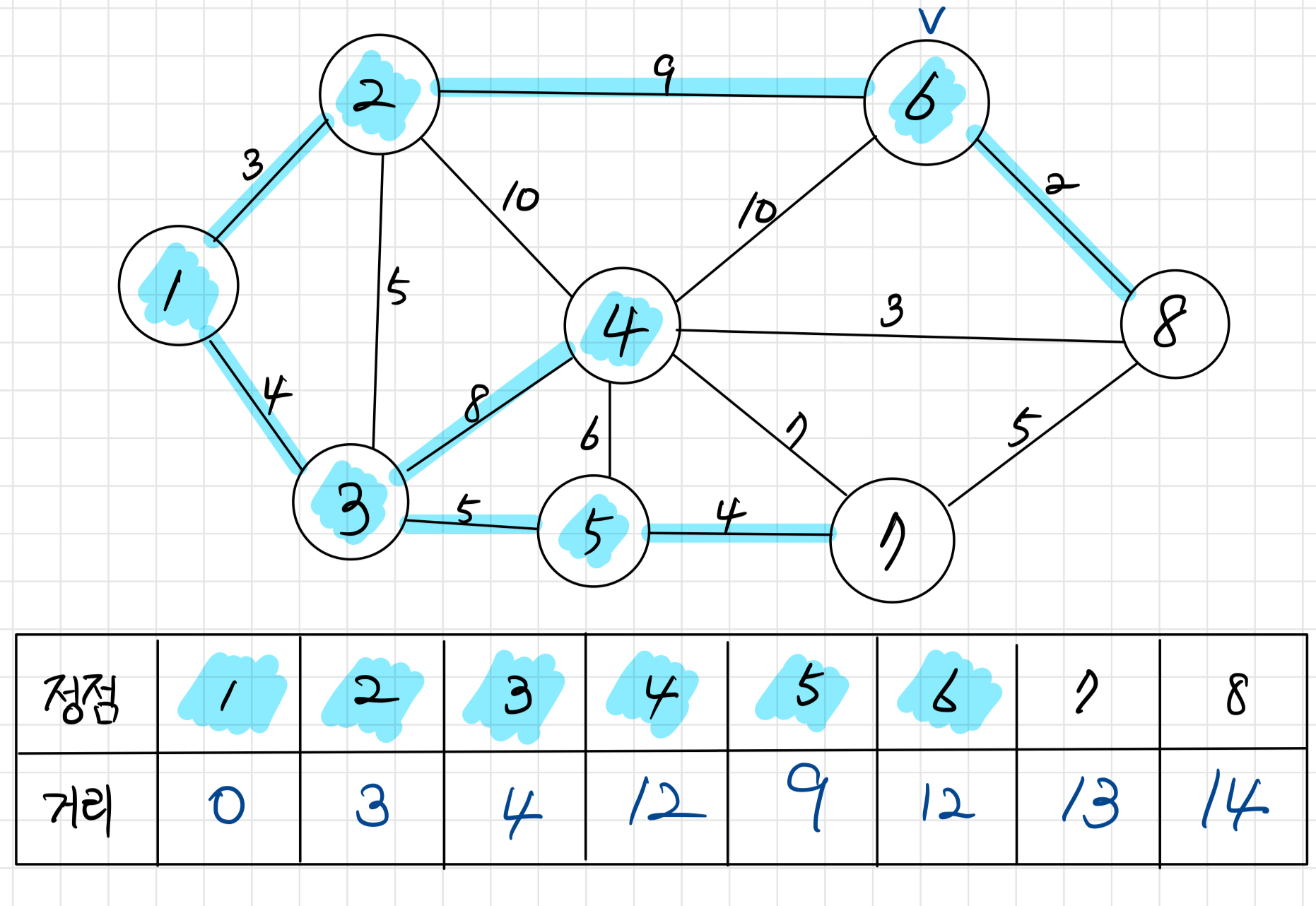
정점 6을 방문한다. 이때도 정점 8까지의 거리를 갱신한다.
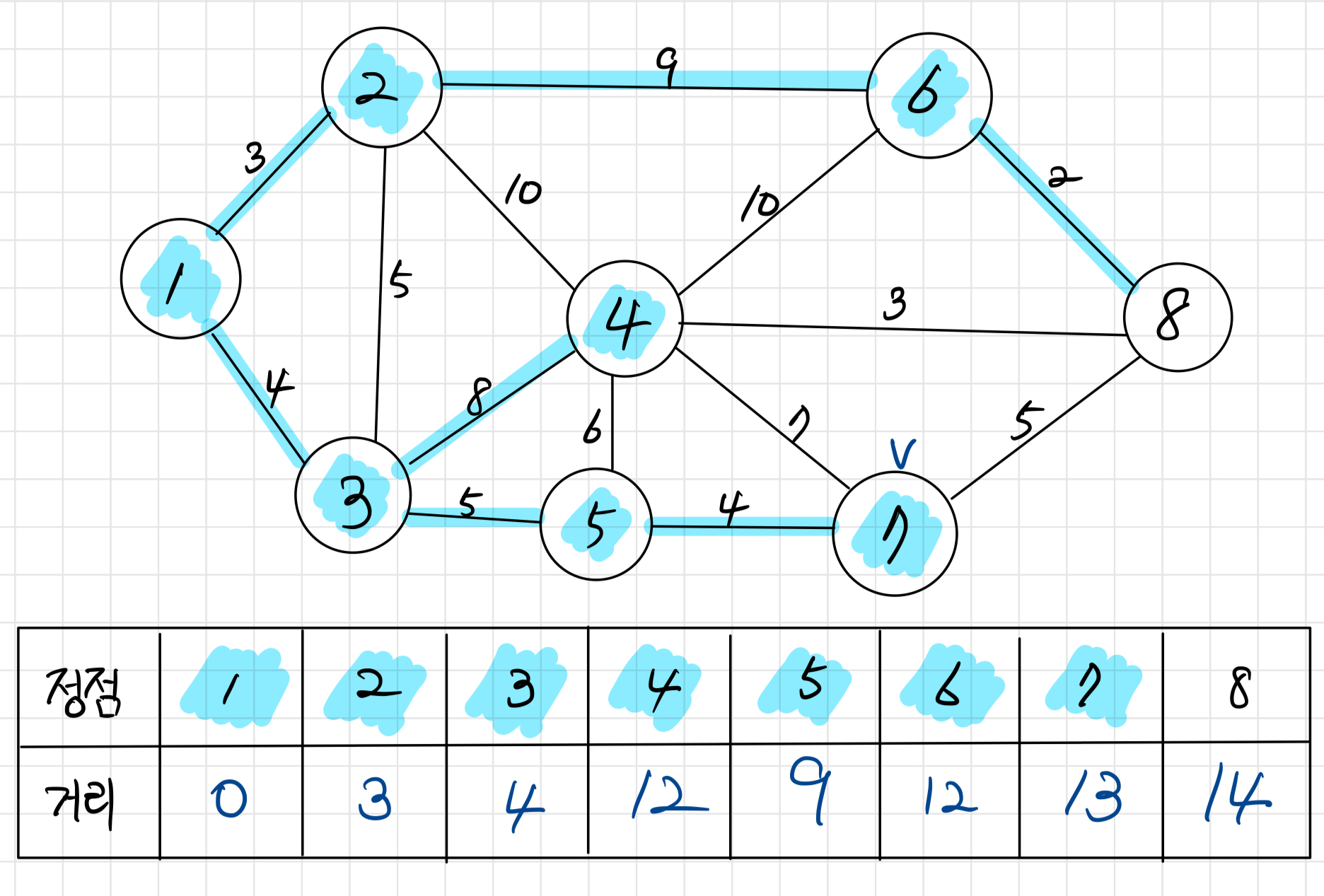
정점 7을 방문한다. 따로 갱신할것은 없다.
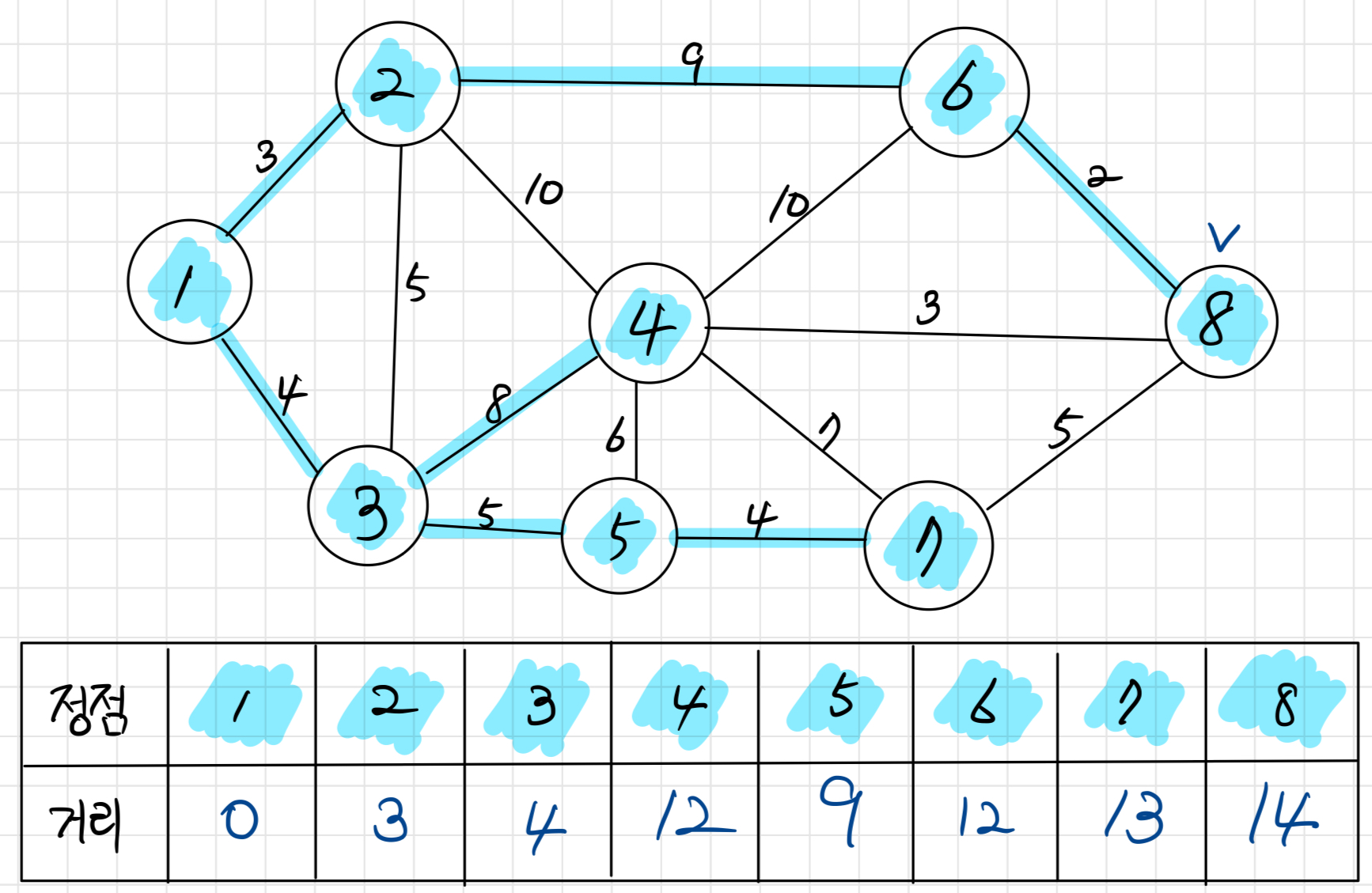
마지막 정점 8을 방문한다. 시작점 1에서 출발하여 갈 수 있는 모든 정점들의 최단 거리가 갱신되었다. 다익스트라 알고리즘을 활용하면 이렇게 특정 출발점에서 각 노드들 까지의 최단거리를 구할 수 있다.
다익스트라 알고리즘 구현
다익스트라 알고리즘을 구현하는 방법은 두 가지가 있는데, 배열을 이용하는 방법과 우선순위 큐를 이용하는 방법이 있다. 정점의 개수를 V, 간선의 개수를 E라고 했을때, 배열을 이용하는 방법은 O(V^2), 우선선위 큐를 이용하는 방법은 O(E logV)의 시간복잡도를 따른다. 우선순위 큐를 이용하는 방법이 훨씬 빠르고 간단하니 필자는 우선순위 큐를 활용하여 구현해보겠다.
#include <iostream>
#include <vector>
#include <queue>
#define MAX 100
#define INF 99999
using namespace std;
int V=8, E=14;
vector<pair<int,int>> Graph[MAX]; //정점과, 정점까지의 거리를 저장한 pair형 vector
int cost[MAX]; //시작점에서 해당 정점까지의 거리를 저장할 배열
void dijkstra(int start) {
cost[start] = 0; //시작점에서 시작점의 거리는 0
priority_queue<pair<int,int>> pq;
pq.push(make_pair(start,0)); //정점과 정점까지의 거리를 우선순위 큐에 push
while (!pq.empty()) {
int current = pq.top().first; //현재 방문 정점
int distance = -pq.top().second; //현재 정점까지의 거리, 음수를 넣어서 가장 작은 수부터 빼도록 설정
pq.pop();
if (cost[current] < distance) continue;
//현재 노드까지의 거리가 저장된 거리보다 크다면 그냥 스킵
for (int i=0; i<Graph[current].size(); i++) { //현재 방문한 정점의 주변 정점 모두 조사
int next = Graph[current][i].first; //현재 정점을 거쳐서 갈 다음 정점
int nextDist = distance + Graph[current][i].second; //현재 정점을 거쳐 다음 정점을 갈때의 거리
if (nextDist < cost[next]) { //기존 거리보다 현재 방문 정점을 거친 거리가 더 작다면
cost[next] = nextDist;
pq.push(make_pair(next, -nextDist));
//cost 배열에 저장된 값 갱신 후 pq에 push
}
}
}
}
int main() {
for (int i=1; i<=E; i++) cost[i] = INF;
//일단 cost배열 INF로 초기화
Graph[1].push_back(make_pair(2,3));
Graph[1].push_back(make_pair(3,4));
Graph[2].push_back(make_pair(1,3));
Graph[2].push_back(make_pair(3,5));
Graph[2].push_back(make_pair(4,10));
Graph[2].push_back(make_pair(6,9));
Graph[3].push_back(make_pair(1,4));
Graph[3].push_back(make_pair(2,5));
Graph[3].push_back(make_pair(4,8));
Graph[3].push_back(make_pair(5,5));
Graph[4].push_back(make_pair(2,10));
Graph[4].push_back(make_pair(3,8));
Graph[4].push_back(make_pair(5,6));
Graph[4].push_back(make_pair(6,10));
Graph[4].push_back(make_pair(7,7));
Graph[4].push_back(make_pair(8,3));
Graph[5].push_back(make_pair(3,5));
Graph[5].push_back(make_pair(4,6));
Graph[5].push_back(make_pair(7,4));
Graph[6].push_back(make_pair(2,9));
Graph[6].push_back(make_pair(4,10));
Graph[6].push_back(make_pair(8,2));
Graph[7].push_back(make_pair(4,7));
Graph[7].push_back(make_pair(5,4));
Graph[7].push_back(make_pair(8,5));
Graph[8].push_back(make_pair(4,3));
Graph[8].push_back(make_pair(6,2));
Graph[8].push_back(make_pair(7,5));
//그래프 생성. vector배열 이용하여 선언, first인자는 목적지, second인자는 목적지 까지의 거리
int startingPoint;
cout << "시작 지점을 입력하세요 : ";
cin >> startingPoint;
dijkstra(startingPoint);
for (int i=1; i<=V; i++) {
cout << "시작점 " << startingPoint << " ~ " << i << "까지의 최단 거리 : " << cost[i] << endl;
}
return 0;
}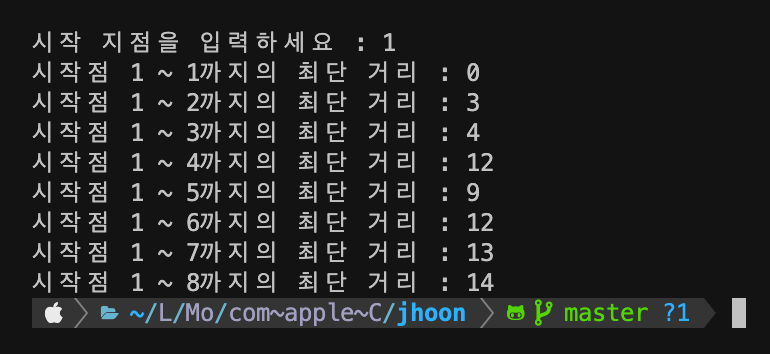
위에서 그렸던 그래프와 같은 그래프로 선언했고, 시작점도 동일하게 설정했다. 결과값을 보면 같은 값들이 나오는 것을 확인할 수 있다.
'Algorithm > 알고리즘 공부' 카테고리의 다른 글
| [알고리즘 공부] 최대공약수와 최소공배수 및 유클리드 호제법 (0) | 2024.03.09 |
|---|---|
| [알고리즘 공부] 그리디 알고리즘 Greedy Algorithm (0) | 2024.03.01 |
| [알고리즘 공부] 프림 알고리즘 Prim's Algorithm (0) | 2024.01.11 |
| [알고리즘 공부] 크루스칼 알고리즘 Kruskal's Algorithm (0) | 2024.01.10 |
| [알고리즘 공부] 너비 우선 탐색 (Breath First Search, BFS) (0) | 2024.01.06 |